|
|
Von Sensor- und
Objektivgrößen - oder -
Einleitung: Man liest es landauf- und landab, digital und in gedruckten Medien: Nur große Bildsensoren können höchste Bildqualitätskriterien erfüllen und auch bei knappem Licht noch gute und rauschfreie Bilder erzeugen. Als Ingenieur in der Optikindustrie mit einer Passion zur Fotografie, neigt man dann teils zum Lachen, weil's zum Weinen schlicht nicht mehr reicht. Daher vier Thesen zur Sinnhaftigkeit großer Bildsensoren für den fortgeschrittenen Foto-Amateur außerhalb des Studios: These 1: 16 Megapixel sind für >90 % der Anwendungen genug. These 2: Das Auflösungsvermögen ist unabhängig von der Sensorgröße, sondern hängt von der Schärfentiefe ab. These 3: Weniger Bildrauschen durch große Sensoren ist nur unter Inkaufnahme kleinerer Schärfentiefe möglich. Bei gleicher Schärfentiefe sind kleine Sensoren im Vorteil. These 4: Weil Sensoren sich flott, Objektive sich hingegen kaum weiter entwickeln, wird das heutige Vollformat/Kleinbildformat das werden, was Mittelformat heute schon ist: Eine Nischenlösung. These 1: 16 Megapixel sind für >90 % der Anwendungen genug
In obigem Graph ist die Entwicklung der jeweils höchsten verfügbaren Sensorauflösung für verschiedene Sensorgrößen in Systemen mit Wechselobjektiv dargestellt. Im Jahr 2024 bietet das Four-Thirds-Format 25 Megapixel, APS-C 40 Megapixel, Kleinbildformat („Vollformat“) 60 Megapixel und die zwei Mittelformate 100 und 150 Megapixel. Nur zur Einordnung liegt ein analoger Farbnegativfilm mit ISO200 im Kleinbild-Format bei ungefähr 14 Megapixel, ein vergleichbarer analoger Mittelformatfilm ungefähr bei 50 Megapixel. Wir können mit digitalen Sensoren also weit mehr Details aufzeichnen, als das analog möglich war. Nur ist das sinnvoll und nötig? Die wenigsten Amateure werden für die militärische Luftaufklärung arbeiten oder Drucke jenseits von DIN A1 (~60x80 cm) anfertigen. Ein typischer Fotoabzug vom Drogeriemarkt löst als 9x13 cm ungefähr 2 Megapixel und als 10x15 cm ungefähr 3 Megapixel auf. Im digitalen Bereich ist das schärfste gängige Wiedergabemedium zur Zeit ein 4k Bildschirm mit ungefähr 8 Megapixel Auflösung (, das blöde 16:9 Seitenverhältnis ignorieren wir einmal). Wobei dort jeder Pixel ganz Foveon-artig aus drei RGB-Subpixeln besteht, was konservativ gerechnet in etwa 16 Megapixeln eines Bayer-Sensors entspricht.
Möchte man Poster anfertigen, sieht man anscheinend den Unterschied zwischen einer 20, einer 50 und 100 Megapixel-Datei erst ab dem A1-Format, zumindest sofern man den direkten Vergleich hat und sehr nah an den Druck heran geht [youtube]. Gemäß myposter benötigt man 60 Pixel pro cm für einen hochqualitativen Druck bzw. 25 Pixel pro cm für ein akzeptables Ergebnis. Eine 20 Megapixel-Datei würde demnach je nach Qualitätsanspruch für Formate von 90x70 cm bis ungefähr 2,2x1,6 m genügen [Quelle]. Neben der Anzeige- bzw. Drucktechnik muss noch das menschliche Auge betrachtet werden, was unter Idealbedingungen nur ca. 1500 Linienpaare pro Bilddiagonale auflösen kann. Umgerechnet auf die Auflösung eines Bayer-Sensors entspricht das ca. 6 Megapixel. Also hat 4k schon einiges an Reserven. Andererseits beschneidet man Bilder auch hin- und wieder, so dass ein mit einem guten Objektiv aufgenommenes (unverwackeltes, unverrauschtes) 16 Megapixel Bild als sinnvolles praktisches Höchstmaß für die breite Masse erscheint. Je nach individuellem Qualitätsbedürfnis könnte man also mit einiger Berechtigung knapp unter oder auch knapp über der 20 Megapixel-Linie in Abb. 1 eine horizontale Linie einzeichnen. Alles über dieser Linie mag zwar in einer Bilddatei vorhanden sein, aber man wird es kaum wiedergeben oder als Mensch wahrnehmen können. Ausnahmen bilden davon Wimmelbilder für den Großformatdruck oder wenn man prinzipiell nur „digital zoomt“. These 2: Das Auflösungsvermögen ist unabhängig von der Sensorgröße, sondern hängt von der Schärfentiefe ab. Selbst wenn man ein ideales
Objektiv ohne jegliche Abbildungsfehler hätte (sowie keinerlei
Fokusrestfehler, kurze Belichtungszeiten bzw. keine Motivbewegung oder
Kamera- erschütterung, keine
Luftschlieren, ...): Am Ende bleibt die Beugungsunschärfe des Objektivs
als absolutes und nicht überwindbares physikalisches Limit. Die
bahnbrechende Theorie dazu stammen von Erst Abbe aus der
Mikroskopie-Welt, übrigens ohne Nobelpreis, und knüpft die
Detailauflösung (Formelzeichen „d“) und die Schärfentiefe („z“)
an die Lichtwellenlänge („l“)
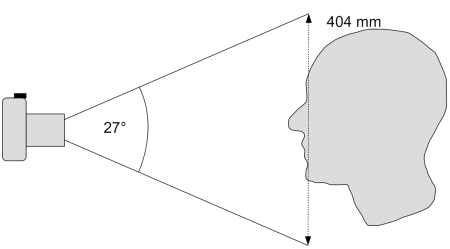
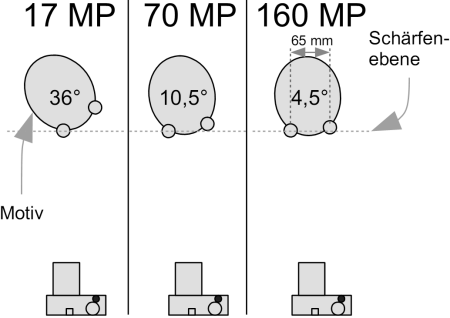
und eine ominöse Numerische Apertur („NA“): Genug der Formelei, wir betrachten lieber ein praktisches Beispiel: Für ein Kopf-Portrait eines Menschen braucht man in etwa eine Bildhöhe von 40 cm Dafür haben wir als Extreme eine Mittelformatkamera mit 53,8x40,3 mm Sensor und sowie eine Four-Thirds-Kameras mit jeweils einem 50 mm kleinbildäquivalentem Objektiv. (Noch extakte Zahlen, für jene, welche nachrechnen wollen: Die Bildhöhe beträgt exakt 40,4 cm und die physikalischen Brennweiten 84,3 mm und 27,1 mm. Menschen und Bildsensoren haben das höchste Auflösungsvermögen bei grünem Licht, so dass die Wellenlänge des Lichts 550 nm beträgt).
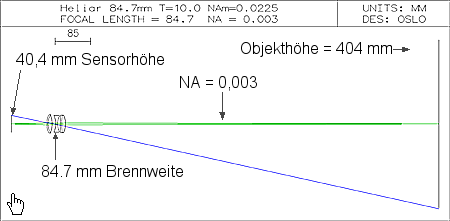
Wir wollen mit beiden Kameras zunächst ein Bild mit einer Auflösung von ca. 17 Megapixel aufnehmen, dafür muss in der Schärfenebene ungefähr alle 0,112 mm ein Bildpunkt aufgelöst werden. Pro Bildpunkt sind das in etwa zwei Haaresbreiten. Rein formal ergibt sich nach Ernst Abbe d = 0,61 · l / NA eine NA von 0,003. Diese ominöse NA ist eine Größe für den Lichtkegel (NA=n·sin(a) mit n=1), welcher vom Motiv ausgeht und vom Objektiv eingefangen wird. In unserem Beispiel hat der Kegel einen Halbwinkel von 0,172° bzw. einen Vollwinkel von 0,344°. Benutzen wir genau diese NA
in einem idealen System ohne jede Fehler, wird theoretisch ein 0,112 mm Hell -
0,112 mm Dunkel - 0,112 mm-Hell-Muster mit immerhin 50 % Kontrast übertragen.
Das sind ca. 9 Tastpunkte pro mm. Die Techniker sprechen gern von
Bildfrequenzen, so dass wir 4,5 Linienpaare pro Millimeter in
unserer Portraitsituation auf den Sensor übertragen können (, da ein
Linienpaar aus einer hellen und dunklen Linie besteht).
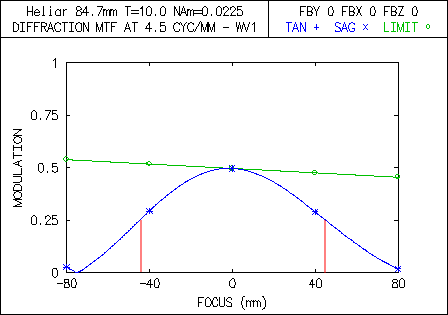
Das Licht läuft in beiden Systemen „rückwärts“, das heißt wir starten links mit der Sensorebene und schauen, welche Bildfrequenz denn durch ein ideales Objektiv auf das Motiv übertragen werden kann. Da der Lichtweg ohnehin umkehrbar ist, ist das Rückwärts-Rechnen ist ein gängiger Rechentrick, um uns die Auswertung weiter unten zu erleichtern. Die Auswertung geschieht über sogenannte MTF-Kurven, wobei wir die Through-Fokus-Variante wählen. In Abb. 6 und 7 ist auf der Abszisse ("x-Achse") der Abstand von der Schärfenebene des Motivs dargestellt und auf der Ordinate ("y-Achse") der Bildkontrast. In der Schärfenebene ("0 mm") ist der Bildkontrast maximal, davor und dahinter sinkt er ab. Diese Funktion wird für die Grenzfrequenz des Sensors aufgetragen, was bei 17 Megapixel ca. 4,5 LP/mm sind. Und siehe da, sofern die NA auf der Seite des Motivs (also rechts vom Objektiv) gleich bleibt, überträgt sowohl das Four-Thirds als auch das Mittelformatsystem die 4,5 Linienpaare pro Millimeter mit dem gleichen Kontrast von 50 %. (Bzw. „vorwärts“ gedacht, kann sowohl das Four-Thirds als auch das Mittelformatsystem den gleichen Detailgrad im Motiv auflösen.). Auch die Schärfentiefe (rote Linie) ist zwischen beiden Systemen gleich. Wir haben ungefähr ± 4 cm Schärfentiefe, d.h. der Kontrast fällt in diesem Bereich um höchstens die Hälfte ab. Die Bilder beider Systeme wären völlig gleich. Wer mit OSLO die MTF-Kurven nachrechnen mag: Der Kommandozeilenbefehl lautet "plm tfo mon 1 4.5 80.0 0 151 y".
So ganz und absolut können eine 4/3s Kamera und ein Mittelformat-System natürlich nicht gleich sein: Die Sensorgröße wirkt sich auf den Bereich zwischen Bildsensor und Objektiv aus, also links vom Objektiv in Abb. 4 und 5. Je kleiner der Sensor, desto größer ist dort der Öffnungswinkel. In der Fotografie benutzen wir statt der NA immer die Blendenzahl k. Für unsere Portraitsituation arbeitet das Four-Thirds-System für 16 Megapixel Auflösung bei Blende 5,3, während das äquivalente Mittelformatsystem auf Blende 16,7 abgeblendet wäre.
Jetzt wäre eine moderne Mittelformatkamera, aber auch eine
Kleinbildkamera mit nur 17 MP Auflösung seitens des Sensors schon
ziemlich unterfordert. Was passiert also, wenn wir die auflösbaren
Bildpunkte im Motiv auf ca. 70 Megapixel vervierfachen, also in jede
Sensorrichtung die doppelte Pixelzahl bedienen?
Jetzt könnte man das Spiel rechnerisch noch auf die Spitze treiben und dem Sensor eine Auflösung von 160 Megapixel anbieten. Hierzu muss die NA nochmal auf 0,009 gesteigert werden, was Blende 1.8 beim idealen Four-Thirds- und Blende 5,6 beim idealen Mittelformat-Objektiv beugungsbegrenzt abbilden muss. An diesem Punkt spielt dann endlich die große Sensorgröße ihren Trumpf aus: Ein beugungsbegrenztes Fotoobjektiv bei Blende 1.8 hätte zu viele Luft-Glas-Flächen. In diesen Regionen geht den kleinen Sensoren dann wirklich endlich die Luft aus. Dieser Zusammenhang zwischen maximaler Auflösung und Blendezahl gilt unabhängig von der Brennweite. Also nicht nur für ein Normalobjektiv, sondern auch für ein leichtes Teleobjektiv. Für alle mathematisch Begeisterten noch die Formeln dazu: Die Auflösung in der Objektebene hängt nur von der NA ab. Der Abbildungsmaßstab G in unserer Portraitsituation beträgt für das Four-Thirds-System -31,08 und für das Mittelformat-System -10,0. Die NA auf Seite des Bildsensors errechnet sich zu: NASensor = -G · NAMotiv Und die Blendenzahl k berechnet sich wie folgt (F16 bedeutet z.B. Blendenzahl k=16): Die physikalisch unabänderliche Kehrseite einer hohen Bildauflösung ist ein drastisches Schrumpfen der Schärfentiefe: Mit dem menschlichen Augenabstand von ungefähr 65 mm kann man für verschiedene Bildauflösungen den maximalen Drehwinkel eines Menschen zur Kamera abschätzen, unter dem auch das hintere Auge noch scharf erscheint. (Bestenfalls fokussieren Kamera ja auf das nahe Auge. Ich kenne keine, die die Mitte zwischen beiden Augen anfokussiert.) Sehr hochauflösende Portraits sind damit quasi auf den direkten Blick in die Kamera festgelegt, was Menschen in sozialer Interaktion mit anderen Menschen (d.h. nicht mit dem Fotograf) erschwert. Aus meiner persönlichen, subjektiven Sicht sind frontale Portraits auf Dauer relativ eintönig und wirken teils wenig lebendig, wie z.B. hier. Im Prinzip bräuchte man Fokus Stacking für Portraits. Lustiger Gedanke.
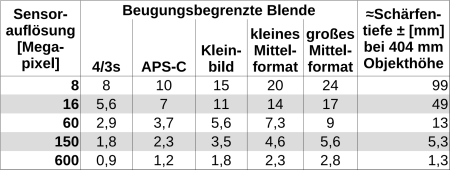
Man kann dieses Spiel verallgemeinern und für jede zur Zeit mögliche Sensorauflösung und jedes Sensorformat die beugungsbegrenzte Blende berechnen. Die geschätzte Schärfentiefe selbst hängt nur von der theoretischen Bildauflösung, nicht jedoch von der Sensorgröße ab (So genau ist die Schärfentiefe-Angabe ohnehin nicht, aber bei den Sensoren mit 3:2 Seitenverhältnis liegt sie eigentlich 10 % höher, da wir hier mit einer festen Bildhöhe und keiner festen Bilddiagonale gerechnet haben.) Interessanter Nebenaspekt: Schon mal gewundert, warum man an einer Pentax *istD oder Olympus E-1 so gut manuell fokussieren kann? Weil die geringe Sensorauflösung eine viel größere Schärfentiefe liefert als eine moderne 16 Megapixel-DSLR:
Die psychologische Frage ist, ob jemand ein monströses Fujifilm X 33 mm F2.3 für 3500 € kaufen würde, wenn es 150 Megapixel Auflösung brächte. Ist doch die "Standardkost" für einen Bruchteil des Preises verfügbar. Und wann braucht man schon mal diese Auflösung? Bei einer Mittelformatkamera scheint diese Hürde wie bei einem Schneider Kreuznach 80 mm F2.8 kleiner zu sein. These 3: Weniger Bildrauschen durch große Sensoren ist nur unter Inkaufnahme kleinerer Schärfentiefe möglich. Bei gleicher Schärfentiefe sind kleine Sensoren im Vorteil. Kern des Punktes ist die Frage, wie stark das Bildrauschen bei knappem Licht zuschlägt, bzw. bis zu welcher Lichtmenge man noch mit akzeptabler Bildqualität fotografieren kann. Im Gegensatz zum vorherigen Abschnitt, geht es hier nicht um möglichst viele Details für DIN A1 Abzüge, sondern um möglichst wenige Störmuster bei moderater Druckgröße. Die Störmuster treten hierbei vor allem in dunklen Bildbereichen auf. Physikalisch hängt die vom Objektiv eingefangene Lichtmenge nur von der Numerischen Apertur (NA) ab, mit der das Motiv betrachtet wird, nicht nicht von der Sensorgröße selbst. Folglich hängt die eingefangene Lichtmenge genauso wie die theoretisch mögliche Bildschärfe rein von der Schärfentiefe ab. Ein Four-Thirds-Objektiv mit Blende 2.0 fängt soviel Licht ein, wie ein Objektiv fürs großes Mittelformat bei Blende 6.3 und hat auch die gleiche Schärfentiefe. Rein physikalisch kompensieren sich die Effekte von geringerer Lichtstärke und größerer Sensorfläche gerade. Praktisch gibt es da jetzt zwei Haken: Erstens ist die Lichtstärke von Objektiven begrenzt, und ich meine damit nicht die absolute Grenze von Blende 0.5. Abb. 12 veranschaulicht den Lichtkegel, welcher bei der jeweiligen Blende auf die Sensormitte fällt. Das praktische Problem dabei: Auf dem Sensor sitzen u.a. ein entspiegeltes Filterglas, eine Mikrolinsen-Schicht, Farbfilter und Antireflex-Schichten direkt auf dem Silizium-Chip und bei Nicht-BSI-Sensoren auch noch die Verdrahtung der Fotozellen. All diese Komponenten sind in ihrem Zusammenspiel nicht für schräg einfallendes Licht ausgelegt und ein wesentlicher Teil des schräg einfallenden Lichts erreicht die Kamerapixel gar nicht mehr. Das führt dazu, dass mitunter die Belichtungszeit beim Öffnen der Blende nicht mehr wesentlich sinkt. [Quelle]. Hinzu kommen ab dem Kleinbildformat Probleme mit dem eigentlich zu kleinen Bajonettdurchmesser, so dass die Bildecken generell nur unter schrägen Winkeln angeleuchtet werden können.
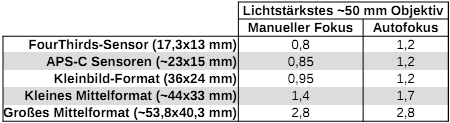
Der zweite praktische Punkt sind die Sensorstörsignale, die eben nicht 1:1 von der eingesammelten Lichtmenge abhängen. Mit der Sensorfläche steigt auch die Siliziumfläche, auf der thermisches Rauschen auftreten kann (wir kühlen Kamerasensoren ja nicht aktiv wie in der Astronomie). Zudem heizen sich große Sensoren stärker auf und es wachsen auch die Signalwege im Sensor. Folglich sind bei gleichem Fertigungs-Know-How kleinere Sensoren bei wirklich richtig knappem Licht etwas besser, als es die reine Physik vermuten lässt [Quelle]. Trotz dessen ist ein großer Sensor ähnlicher Fertigungstechnik bei gleichem ISO-Wert natürlich deutlich rauschärmer als ein kleiner Sensor. Das praktisch entscheidende Merkmal für Fotos bei richtig richtig knappem Licht ist die Verfügbarkeit von entsprechenden Objektiven. Autofokus würde ich aufgrund der sehr kleinen Schärfentiefe als nötig voraussetzen. Mit AF gibt es herstellerübergreifend mit Ausnahme des Fujinon XF 50 mm F1.0 bestenfalls Blende 1.2. Und bei gleicher Blende ist nunmal der größte Sensor am rauschärmsten, was zur Zeit das Kleinbildformat ist. Dicht gefolgt vom kleinen Mittelformat (Fujifilm G).
Jetzt geht es bei hochgeöffneten Objektiven wie F1.2 oder F0.95 oft nicht nur um die Menge der gesammelten Photonen, sondern auch um eine möglichst dünne Schärfenebene und entsprechend verschmierten Vor- und Hintergrund. Sofern man darauf steht, und nicht lieber den Hintergrund verschmiert, ohne die Schärfenebene superdünn werden zu lassen, ist auch hier ein Kleinbildsensor das Mittel der Wahl. Bei Anwendungen mit sehr geringen Schärfentiefeanforderungen wie der Astrofotografie ohnehin. Ist man hingegen ohnehin auf eine etwas größere Schärfentiefe angewiesen (um z.B. mehrere Personen im Fokus zu halten oder zumindest beide Augen einer Person), sind tendenziell die kleinen Sensoren im Vorteil. Dort kommen dann vor allem die geringeren Störsignale aufgrund der kleineren Sensorfläche zum Tragen. These 4: Weil Sensoren sich flott, Objektive sich hingegen kaum weiter entwickeln, wird das heutige Vollformat/Kleinbildformat das werden, was Mittelformat heute schon ist: Eine Nischenlösung. Als Bildqualität wird die Abwesenheit von Makeln wie Sensorrauschen oder Farbquerfehler bei gleichzeitig hoher Bildauflösung definiert. Folglich müssen die Imperfektionen der Abbildung (also Objektivfehler) und die Imperfektionen der Sensoren (begrenzte Auflösung, Rauschen) in einem Gleichgewicht stehen. Oder praktisch formuliert: Ein Objektiv, das an einem APS-C-Sensor mit nur 6 MP gut auflöst, kann von einem modernen 40 MP APS-C Sensor heillos überfordert sein.
Sensoren profitieren von der insgesamt rasanten Entwicklung der Halbleiterindustrie. Binnen zwanzig Jahren ist Qualität bei gleicher Baugröße deutlich gestiegen, sowohl was die Bildauflösung ("Megapixel") als auch das Bildrauschen ("ISO") betrifft. Bzw. für die gleiche Bildqualität reicht heute eine viel kleinere Sensorfläche als vor 10 Jahren [Quelle]. Das hat viel mit der Miniaturisierung von Transistoren, mit neuen Fertigungsverfahren für die Back-Side-Illumination und mit neuen chemischen Materialien für die Farbfiltern der Bayermatrix zu tun. Die Bildqualität ist zwischenzeitlich so gut, dass man dort sogar bewusst Abstriche zugunsten schneller Auslesung oder Fokus-Funktionen (Stacked-Sensoren, Dual- oder Quad-Pixel-AF) bzw. für einen elektronischen Verschluss bei Global Shutter Sensoren in Kauf nimmt. Und solange das Ausleserauschen, und nicht das Schrot-Rauschen der Photonen, die Störsignale dominiert, ist dort die physikalische Grenze auch noch nicht erreicht. Die Objektive bestehen hingegen bestehen wie vor 50 Jahren immer noch hauptsächlich aus sphärischen Glaslinsen (für den Laien: Ein Glaskörper mit zwei anpolierten Kugelflächen) und arbeiten nah am erreichbaren physikalischen bzw. glastechnischen Limit. Einzig die DO-Technologie von Canon (bzw. Phase Fresnel von Nikon) sind echte technologische Durchbrüche, aber bisher leider nur für den Super-Telebereich geeignet. Anderer Technologiedurchbrüche sehe ich zur Zeit nicht am Horizont, so dass bei ähnlichem Bauraum ähnliche Ergebnisse wie vor 50 Jahren erreicht werden [Quelle]. Bessere Abbildungsleistungen ergeben sich nur noch durch bessere Antireflex-Schichten, gesunkene Kosten für höhere Fertigungsgenauigkeit und gesunkene Kosten für Asphären. Sprich, wenn man Linsen genauer fertigt und auch genauer im Objektiv anordnet und bewegt, wird die Bildqualität besser (und man kann mit mehr Linsen im Objektiv auch schärfere Bilder erzeugen). Die Kehrseite davon ist natürlich, dass dieser Weg sowohl die Preise als auch Gewicht und Volumen nach oben treibt. Zu Veranschaulichung: Für die industrielle Chip-Fertigung benötigt man im Prinzip Makroobjektive mit einer festen Vergrößerung von 1:4, die bei einer Laserwellenlänge von 193,35 nm arbeiten. Um die gewünschte Abbildungsleistung zu erreichen, ist schlicht ein immenses Stapel an Linsen mit entsprechend hochgenauen Fassungen nötig, was zu einem in Volumen und Gewicht monströsen Objektiv führt:
Aus Nutzersicht wird die technologische Stagnation in der Optik durch den einmaligen Übergang von der Spiegelreflex zum spiegellosen System temporär kaschiert, da durch die Reduktion des Auflagemaßes mehr geometrischen Raum für die Optikdesigner zur Verfügung steht. Das ist jedoch ein Einmaleffekt ohne Wiederkehr. Das Problem wird erst so richtig klar, wenn man ein „beständiges Systeme“ wie Leica M oder Pentax K betrachtet. Dort sind die Objektive der frühen 2000er nicht wesentlich schlechter als heutige, zwischen einer Epson R-D1 und einer Leica M11 oder eine Pentax *istD und einer K3 III liegen jedoch nicht nur in der Bildqualität Welten. Ich würde jedenfalls lieber das alte Objektiv mit der neusten Kamera nehmen, wenn ich gute Fotos abliefern muss und nicht nur aus Liebhaberei fotografiere.
Für ältere Fotografen mag es erst einmal komisch erscheinen, dass heute ein modernes 50 mm Objektiv wie das Nikon Z 50 mm F1.2 S trotz „nur" Blende 1.2 glatt 15 cm lang und 1 kg schwer ist. Jedoch ist diese Größe schlicht nötig, um bei Offenblende nicht ins Bodenlose zu stürzen und drei Blenden abgeblendet zumindest so halbwegs einen 46 MP Kleinbildsensor bedienen zu können. Und wir reden hier wohlgemerkt über Festbrennweiten, nicht über Zooms. Ein klassisches 50 mm F1.2 für den analogen Film hat in etwa die Maße des links dargestellten Nikon 40 mm F2.0.
Noch gravierender wird das Thema im Bereich der Zooms. Im Mittelformatbereich, wo Preise nicht ganz so wichtig ist, sind Zoomfaktoren von 2x die Regel. Alles darüber hinaus wäre entweder zu unscharf oder zu groß. Wenn Kleinbildkameras zukünftig höher auflösen, dann werden entweder die ohnehin schon großen Zoomobjektive noch größer werden oder die Zoomfaktoren werden kleiner, also die Zooms weniger praxistaulich. Für die kleinen Sensoren, APS-C und Four-Thirds, sieht die Perspektive dort wesentlich günstiger aus, da die benötigten Auflösungen dort erstens niedriger sind und auch die Objektive oft noch halbwegs kompakt und tragbar. Schreibt man die Entwicklung der Bildsensoren in die Zukunft fort, so könnten wir in 10 Jahren die Pixelzahl um 30 bis 50 % steigern, sofern keine Smartphone-Technik Einzug hält, die das noch weiter beschleunigen würde. Nur welches Standardzoom soll einen 100 Megapixel Kleinbildsensor adäquat bedienen können? Und warum sollte man das mitschleppen, wo man diese Bildauflösung kaum jemals wirklich benötigen wird? Langfristig könnte man sich verschiedene konstruktive Lösungsansätze für diese disparate Entwicklung zwischen Sensorik und Optik überlegen:
Vielleicht liegt es in der Natur des Menschen, Dinge zu kaufen, welche absehbar keinen praktischen Nutzen haben. Wenn PKW in Spanien in der Regel für deutlich jenseits der 130 km/h ausgelegt sind, muss Deutschland aus deren Sicht ein sehr attraktives Urlaubsland sein. Beim Hype um Kamerasysteme mit großen Sensoren, ist das aus meiner Sicht kaum anders. Zumindest bis wir alle Neuroimplantate haben, um die lästige menschliche Wahrnehmungsbarriere von nur 6 Megapixel zu überbrücken. Mai 2024 |